
Décroissance radioactive
Une désintégration radioactive est un phénomène aléatoire sur lequel il est impossible d’agir : il n’existe aucun facteur permettant de modifier ces caractéristiques. La probabilité de désintégration d’un noyau est la même à chaque instant dans un intervalle de temps donné. Elle ne dépend pas du passé ou des désintégrations précédentes. De plus, elle n’influence pas les autres noyaux de l’échantillon. Le caractère aléatoire est à l’origine de la loi d’évolution temporelle d’un ensemble de noyaux radioactifs : la loi de décroissance radioactive.
Loi de décroissance
On part d’un nombre de N(t) nombre de noyau radioactif, à un instant donné dans un échantillon. Pendant une durée Δ(t) le nombre de noyau radioactif diminue et passe de N à N + ΔN, avec ΔN < 0
Donc il y a une désintégration de -ΔN noyaux
La probabilité pour que -ΔN noyaux se soient désintégrés pendant Δt correspond à -ΔN /N.
Or, la probabilité pour que -ΔN noyaux se soient désintégrés pendant la durée Δt est proportionnelle à Δt.
Donc -ΔN / N = λ Δt ou ΔN / Δt = - λN avec λ la constante de désintégration > 0.
La loi de décroissance est obtenue par l’utilisation de la fonction exponentielle décroissante qui décrit l’évolution temporel du nombre de noyaux radioactifs de l’échantillon.
-λt
N(t) N0 e
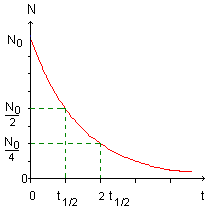
Courbe de décroissance / demi-vie
D’après la loi de décroissance, à l’instant T= 1/λ, le nombre de noyaux radioactifs est égal à N0 e-1 est 0,37 N0.
Une autre grandeur est utilisée pour caractériser le comportement d’un échantillon radioactif : la demi vie t1/2.
Après celle-ci, la moitié de la quantité de matière du noyau radioactif contenu dans les échantillons s’est désintégrée.
Activité radioactive
A0 est l'activité initiale de l’échantillon à l’instant t = 0
- λxt
A(t) = A0 x e
La courbe donnant l’activité en fonction du temps est la même que celle donnant le nombre N(t) de noyaux radioactifs en fonction du temps. Comme A(t) = λ x N(t), l’activité de l’échantillon à l’instant t est proportionnelle au nombre N(t) de noyaux radioactifs contenus dans celui-ci à cet instant et à la constante de radioactivité. Elle est donc proportionnelle à l’inverse de la demi-vie t1/2.
Remarque : parmi deux échantillons différents ayant le même nombre de noyaux radioactifs, celui qui a la demi-vie la plus courte, a une plus grande activité.
